Import packages and define constants
import os
import tensorflow as tf
import numpy as np
from sklearn.model_selection import train_test_split
from sklearn.metrics import precision_recall_fscore_support
import matplotlib.pyplot as plt
# Plots
%matplotlib inline
font = {
'family' : 'serif',
'weight' : 'normal',
'size' : 12
}
plt.rc('font', **font)
PDF= True # A boolean value speficifying whether the figures should be exported to PDF
# System information
# ieee14: 27 components
# ieee57: 100 components
SYS = 'ieee14'
N_COMP = 27 # Number of components in the system
# Input files
SEQ_DIR = 'failure_seq'
INIT_FILE = os.path.join(SEQ_DIR, SYS + '_smart_initial.txt')
RESULT_FILE = os.path.join(SEQ_DIR, SYS + '_smart_result.txt')
CMPLX_INIT_FILE = os.path.join(SEQ_DIR, SYS + '_smart_cmplx_initial.txt')
CMPLX_RESULT_FILE = os.path.join(SEQ_DIR, SYS + '_smart_cmplx_result.txt')
# Neural network
N_STEPS = 5000 # Number of training steps
REC_INT = 100 # Number of steps between recording measures
VERBOSE = True # A boolean value speficifying whether the performance measures should be printed every REC_INT steps
BATCH_SIZE = 128 # Size of the batch for training
N_HIDDEN_L = 256 # Number of nodes in outer hidden layers
N_HIDDEN_M = 128 # Number of nodes in middle hidden layers
N_HIDDEN_S = 64 # Number of nodes in centeral hidden layers
TEST_SIZE = 0.10 # Portion of data to be used for testing
VALID_SIZE = 0.10 # Portion of data to be used for validation
LEARNING_RATE = 0.005 # Ratio of knowledge to learn at each new step as compared to previously established knowledge
REGULATION_RATE = 2e-6 # Penalizing factor for increased weights (prevents overfitting)
FAILURE_THRESHOLD = 0.90 # Threshold for deciding failed/functional state for components in the predictions
SEED = 1818 # Seed for random number generators
Read initial and resulting failures
init_data = np.zeros((1, N_COMP))
with open(INIT_FILE, 'r') as init_file:
for i, line in enumerate(init_file):
indices = line.split()
l = np.zeros((1, N_COMP))
if len(indices) > 1:
l[0, indices[1:]] = 1
init_data = np.append(init_data, l, 0)
if os.path.isfile(CMPLX_INIT_FILE):
cmplx_init_data = np.zeros((0, N_COMP))
with open(CMPLX_INIT_FILE, 'r') as cmplx_init_file:
for i, line in enumerate(cmplx_init_file):
indices = line.split()
l = np.zeros((1, N_COMP))
if len(indices) > 1:
l[0, indices[1:]] = 1
cmplx_init_data = np.append(cmplx_init_data, l, 0)
result_data = np.zeros((1, N_COMP))
with open(RESULT_FILE, 'r') as result_file:
for i, line in enumerate(result_file):
indices = line.split()
l = np.zeros((1, N_COMP))
if len(indices) > 1:
l[0, indices[1:]] = 1
result_data = np.append(result_data, l, 0)
if os.path.isfile(CMPLX_RESULT_FILE):
cmplx_result_data = np.zeros((0, N_COMP))
with open(CMPLX_RESULT_FILE, 'r') as cmplx_result_file:
for i, line in enumerate(cmplx_result_file):
indices = line.split()
l = np.zeros((1, N_COMP))
if len(indices) > 1:
l[0, indices[1:]] = 1
cmplx_result_data = np.append(cmplx_result_data, l, 0)
print('Simple dataset: {}, Complex dataset: {}'.format(init_data.shape[0], cmplx_init_data.shape[0]))
/usr/local/lib/python3.5/dist-packages/ipykernel/__main__.py:7: VisibleDeprecationWarning: non integer (and non boolean) array-likes will not be accepted as indices in the future
/usr/local/lib/python3.5/dist-packages/ipykernel/__main__.py:17: VisibleDeprecationWarning: non integer (and non boolean) array-likes will not be accepted as indices in the future
/usr/local/lib/python3.5/dist-packages/ipykernel/__main__.py:26: VisibleDeprecationWarning: non integer (and non boolean) array-likes will not be accepted as indices in the future
Simple dataset: 17969, Complex dataset: 1423
/usr/local/lib/python3.5/dist-packages/ipykernel/__main__.py:36: VisibleDeprecationWarning: non integer (and non boolean) array-likes will not be accepted as indices in the future
Split data to training, test, and validation
x_train_valid, x_test, y_train_valid, y_test = train_test_split(
init_data, result_data, test_size=int(TEST_SIZE*init_data.shape[0]), random_state=SEED)
x_train, x_valid, y_train, y_valid = train_test_split(
x_train_valid, y_train_valid, test_size=int(VALID_SIZE*init_data.shape[0]), random_state=SEED)
x_cmplx_test, y_cmplx_test = cmplx_init_data, cmplx_result_data
print('Training: {}, Validation: {}, Test: {}, Complex Test: {}'.format(
x_train.shape[0], x_valid.shape[0], x_test.shape[0], x_cmplx_test.shape[0]))
Training: 14377, Validation: 1796, Test: 1796, Complex Test: 1423
Classification and performance
def decision(predictions, threshold=0.5):
if isinstance(predictions, float):
return predictions > threshold
elif predictions.ndim == 1:
return predictions > threshold * 1 #np.amax(predictions)
elif predictions.ndim == 2:
return predictions > threshold * 1 #np.amax(predictions, 1)[np.newaxis].T
return None
def performance(actual, predictions_bin, beta=1):
act = np.empty(shape=[0, actual.shape[1]])
pre = np.empty(shape=[0, predictions_bin.shape[1]])
for i in range(actual.shape[0]):
if any(actual[i, :]) and any(predictions_bin[i, :]):
act = np.append(act, actual[i, :][np.newaxis], 0)
pre = np.append(pre, predictions_bin[i, :][np.newaxis], 0)
accuracy = np.sum(predictions_bin == actual) / predictions_bin.size
if act.size > 0 and pre.size > 0:
precision, recall, fscore, _ = precision_recall_fscore_support(
act, pre, average='samples', beta=beta)
else:
precision, recall, fscore = (0, 0, 0)
return {'accuracy': accuracy, 'precision': precision, 'recall': recall, 'fscore': fscore}
Neural network model
graph = tf.Graph()
with graph.as_default():
# Inputs
tf_train_dataset = tf.placeholder(shape=(BATCH_SIZE, N_COMP), dtype=tf.float64)
tf_train_labels = tf.placeholder(shape=(BATCH_SIZE, N_COMP), dtype=tf.float64)
tf_valid_dataset = tf.constant(x_valid)
tf_valid_labels = tf.constant(y_valid)
tf_test_dataset = tf.constant(x_test)
tf_test_labels = tf.constant(y_test)
tf_cmplx_test_dataset = tf.constant(x_cmplx_test)
tf_cmplx_test_labels = tf.constant(y_cmplx_test)
# Layer 1
weights_1 = tf.get_variable("weights_1", shape=[N_COMP, N_HIDDEN_L],
initializer=tf.contrib.layers.xavier_initializer(), dtype=tf.float64)
biases_1 = tf.Variable(tf.zeros([N_HIDDEN_L], dtype=tf.float64))
# Layer 2
weights_2 = tf.get_variable("weights_2", shape=[N_HIDDEN_L, N_HIDDEN_M],
initializer=tf.contrib.layers.xavier_initializer(), dtype=tf.float64)
biases_2 = tf.Variable(tf.zeros([N_HIDDEN_M], dtype=tf.float64))
# Layer 3
weights_3 = tf.get_variable("weights_3", shape=[N_HIDDEN_M, N_HIDDEN_S],
initializer=tf.contrib.layers.xavier_initializer(), dtype=tf.float64)
biases_3 = tf.Variable(tf.zeros([N_HIDDEN_S], dtype=tf.float64))
# Layer 4
weights_4 = tf.get_variable("weights_4", shape=[N_HIDDEN_S, N_HIDDEN_M],
initializer=tf.contrib.layers.xavier_initializer(), dtype=tf.float64)
biases_4 = tf.Variable(tf.zeros([N_HIDDEN_M], dtype=tf.float64))
# Layer 5
weights_5 = tf.get_variable("weights_5", shape=[N_HIDDEN_M, N_HIDDEN_L],
initializer=tf.contrib.layers.xavier_initializer(), dtype=tf.float64)
biases_5 = tf.Variable(tf.zeros([N_HIDDEN_L], dtype=tf.float64))
# Output layer
weights_out = tf.get_variable("weights_out", shape=[N_HIDDEN_L, N_COMP],
initializer=tf.contrib.layers.xavier_initializer(), dtype=tf.float64)
biases_out = tf.Variable(tf.zeros([N_COMP], dtype=tf.float64))
def model(input_data):
activation_1 = tf.nn.relu(tf.matmul(input_data, weights_1) + biases_1)
activation_2 = tf.nn.relu(tf.matmul(activation_1, weights_2) + biases_2)
activation_3 = tf.nn.relu(tf.matmul(activation_2, weights_3) + biases_3)
activation_4 = tf.nn.relu(tf.matmul(activation_3, weights_4) + biases_4)
activation_5 = tf.nn.relu(tf.matmul(activation_4, weights_5) + biases_5)
return activation_5
# Training
activation_model = model(tf_train_dataset)
logits_train = tf.matmul(activation_model, weights_out) + biases_out
loss_train = (tf.reduce_mean(tf.nn.sigmoid_cross_entropy_with_logits(logits_train, tf_train_labels)) +
REGULATION_RATE * tf.nn.l2_loss(weights_1))
# Optimizer
# TODO - Try other optimizers and adjust learning rate. Weight decay is an option
optimizer = tf.train.AdamOptimizer(LEARNING_RATE).minimize(loss_train)
# Predictions
logits_valid = tf.matmul(model(tf_valid_dataset), weights_out) + biases_out
loss_valid = tf.reduce_mean(tf.nn.sigmoid_cross_entropy_with_logits(logits_valid, tf_valid_labels))
sigmoid_valid = tf.nn.sigmoid(logits_valid)
logits_test = tf.matmul(model(tf_test_dataset), weights_out) + biases_out
sigmoid_test = tf.nn.sigmoid(logits_test)
logits_cmplx_test = tf.matmul(model(tf_cmplx_test_dataset), weights_out) + biases_out
sigmoid_cmplx_test = tf.nn.sigmoid(logits_cmplx_test)
Train the neural network
with tf.Session(graph=graph) as session:
tf.global_variables_initializer().run()
ls_train_log = []
ls_valid_log = []
perf_valid_log = []
print('Training the network...')
for step in range(N_STEPS + 1):
offset = (step * BATCH_SIZE) % (y_train.shape[0] - BATCH_SIZE)
batch_data = x_train[offset:(offset + BATCH_SIZE), :]
batch_labels = y_train[offset:(offset + BATCH_SIZE), :]
feed_dict = {tf_train_dataset : batch_data, tf_train_labels : batch_labels}
_, ls_train, ls_valid, sg_valid = session.run(
[optimizer, loss_train, loss_valid, sigmoid_valid], feed_dict=feed_dict)
ls_train_log.append(ls_train)
ls_valid_log.append(ls_valid)
perf_valid = performance(y_valid, decision(sg_valid, FAILURE_THRESHOLD))
perf_valid_log.append(perf_valid)
if (VERBOSE and step == 0):
print('Step\tTR-Loss\t\tVL-Loss\t\tAccuracy\tRecall\t\tPrecision\tF-Score')
print('-' * 95)
if VERBOSE and step % REC_INT == 0:
print((
'{step:5d}\t'
'{tr_loss:.4f}\t\t'
'{vl_loss:.4f}\t\t'
'{p[accuracy]:.2%}\t\t'
'{p[recall]:.2%}\t\t'
'{p[precision]:.2%}\t\t'
'{p[fscore]:.2%}').format(
step=step,
tr_loss=ls_train,
vl_loss=ls_valid,
p=perf_valid)
)
if VERBOSE:
print('-' * 95)
sg_test = sigmoid_test.eval()
print(5 * '\t' + 'Accuracy\tRecall\t\tPrecision\tF-Score')
print((
'Test Dataset:\t\t\t\t'
'{p[accuracy]:.2%}\t\t'
'{p[recall]:.2%}\t\t'
'{p[precision]:.2%}\t\t'
'{p[fscore]:.2%}').format(
p=performance(y_test, decision(sg_test, FAILURE_THRESHOLD)))
)
if VERBOSE:
print('-' * 95)
sg_cmplx_test = sigmoid_cmplx_test.eval()
print(5 * '\t' + 'Accuracy\tRecall\t\tPrecision\tF-Score')
print((
'More Complex Test Dataset:\t\t'
'{p[accuracy]:.2%}\t\t'
'{p[recall]:.2%}\t\t'
'{p[precision]:.2%}\t\t'
'{p[fscore]:.2%}').format(
p=performance(y_cmplx_test, decision(sg_cmplx_test, FAILURE_THRESHOLD)))
)
Training the network...
Step TR-Loss VL-Loss Accuracy Recall Precision F-Score
-----------------------------------------------------------------------------------------------
0 0.6919 0.6556 99.40% 0.00% 0.00% 0.00%
100 0.0120 0.0312 99.40% 100.00% 100.00% 100.00%
200 0.0009 0.0508 99.43% 71.65% 81.33% 74.46%
300 0.0002 0.0576 99.45% 70.42% 79.48% 73.26%
400 0.0002 0.0612 99.45% 71.92% 81.35% 74.81%
500 0.0002 0.0627 99.45% 71.01% 79.20% 73.44%
600 0.0002 0.0647 99.46% 72.13% 79.89% 74.43%
700 0.0001 0.0656 99.47% 73.18% 79.68% 75.08%
800 0.0001 0.0664 99.47% 74.16% 80.81% 76.12%
900 0.0001 0.0669 99.47% 74.25% 80.61% 76.07%
1000 0.0001 0.0673 99.47% 73.79% 80.52% 75.77%
1100 0.0001 0.0675 99.48% 73.83% 80.36% 75.75%
1200 0.0001 0.0676 99.48% 74.80% 81.03% 76.59%
1300 0.0011 0.0666 99.49% 75.08% 80.79% 76.64%
1400 0.0008 0.0664 99.47% 74.98% 82.19% 77.20%
1500 0.0001 0.0722 99.44% 66.79% 73.91% 68.79%
1600 0.0001 0.0654 99.47% 74.57% 80.13% 76.24%
1700 0.0001 0.0670 99.48% 75.54% 80.43% 77.00%
1800 0.0001 0.0676 99.49% 76.54% 81.25% 77.91%
1900 0.0001 0.0677 99.49% 77.88% 82.64% 79.25%
2000 0.0001 0.0676 99.49% 77.35% 81.99% 78.63%
2100 0.0001 0.0676 99.49% 78.44% 83.04% 79.73%
2200 0.0000 0.0676 99.49% 77.66% 82.26% 79.00%
2300 0.0000 0.0676 99.49% 77.61% 82.12% 78.88%
2400 0.0000 0.0679 99.50% 77.23% 82.14% 78.63%
2500 0.0000 0.0678 99.49% 77.42% 82.06% 78.72%
2600 0.0000 0.0680 99.49% 77.50% 82.10% 78.73%
2700 0.0000 0.0680 99.49% 76.88% 81.82% 78.25%
2800 0.0000 0.0683 99.49% 77.18% 82.11% 78.55%
2900 0.0000 0.0685 99.50% 77.52% 82.34% 78.79%
3000 0.0000 0.0690 99.50% 77.10% 82.37% 78.55%
3100 0.0000 0.0692 99.50% 77.51% 82.39% 78.87%
3200 0.0000 0.0698 99.50% 77.99% 82.55% 79.20%
3300 0.0673 0.1547 99.35% 51.40% 56.82% 52.68%
3400 0.0005 0.0612 99.42% 65.62% 71.94% 67.56%
3500 0.0004 0.0629 99.42% 64.28% 70.77% 66.19%
3600 0.0003 0.0655 99.42% 65.59% 72.34% 67.58%
3700 0.0004 0.0676 99.43% 66.89% 73.60% 68.84%
3800 0.0003 0.0714 99.43% 67.78% 74.27% 69.66%
3900 0.0002 0.0739 99.44% 68.00% 73.97% 69.72%
4000 0.0002 0.0758 99.44% 68.74% 74.64% 70.42%
4100 0.0002 0.0776 99.43% 68.71% 74.53% 70.36%
4200 0.0002 0.0790 99.44% 69.08% 74.75% 70.68%
4300 0.0002 0.0803 99.44% 69.52% 75.38% 71.19%
4400 0.0002 0.0814 99.44% 69.77% 75.59% 71.43%
4500 0.0001 0.0825 99.44% 70.22% 75.98% 71.87%
4600 0.0001 0.0835 99.44% 70.93% 76.51% 72.51%
4700 0.0001 0.0845 99.44% 70.68% 76.34% 72.28%
4800 0.0001 0.0855 99.44% 69.30% 75.35% 71.00%
4900 0.0001 0.0861 99.44% 69.64% 75.64% 71.31%
5000 0.0001 0.0868 99.44% 69.98% 75.84% 71.61%
-----------------------------------------------------------------------------------------------
Accuracy Recall Precision F-Score
Test Dataset: 99.45% 70.29% 75.99% 72.01%
-----------------------------------------------------------------------------------------------
Accuracy Recall Precision F-Score
More Complex Test Dataset: 98.87% 53.56% 63.99% 55.93%
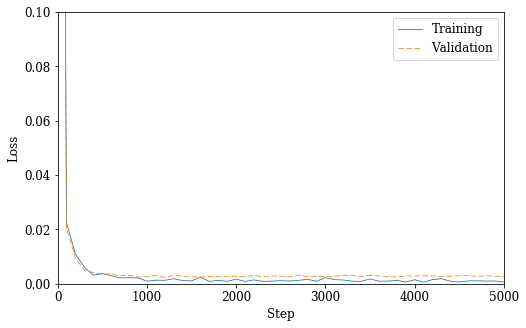
Performance over training epochs
acc_log = [x['accuracy'] for x in perf_valid_log[0::REC_INT]]
rec_log = [x['recall'] for x in perf_valid_log[0::REC_INT]]
pre_log = [x['precision'] for x in perf_valid_log[0::REC_INT]]
fsc_log = [x['fscore'] for x in perf_valid_log[0::REC_INT]]
n = len(ls_train_log) // REC_INT
x = np.arange(0, REC_INT * n + 1, REC_INT)
fig_loss = plt.figure(figsize=(8, 5))
plt.plot(x, ls_train_log[0::REC_INT], '-C0', x, ls_valid_log[0::REC_INT], 'C1--', linewidth=0.8)
plt.xlabel('Step')
plt.ylabel('Loss')
plt.xlim(0, REC_INT * n)
plt.ylim(0, 0.1)
plt.legend(('Training', 'Validation'))
plt.show()
if PDF:
fig_loss.savefig(SYS + '_nn_loss.pdf', bbox_inches='tight')
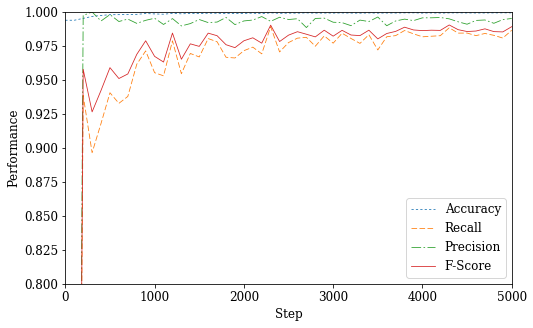
fig_perf = plt.figure(figsize=(8, 5))
acc_max = (REC_INT * np.argmax(acc_log), np.amax(acc_log))
rec_max = (REC_INT * np.argmax(rec_log), np.amax(rec_log))
pre_max = (REC_INT * np.argmax(pre_log), np.amax(pre_log))
fsc_max = (REC_INT * np.argmax(fsc_log), np.amax(fsc_log))
plt.plot(x, acc_log, ':C0',
#acc_max[0], acc_max[1], 'C0s',
x, rec_log, '--C1',
#rec_max[0], rec_max[1], 'C1s',
x, pre_log, '-.C2',
#pre_max[0], pre_max[1], 'C2s',
x, fsc_log, '-C3',
#fsc_max[0], fsc_max[1], 'C3s'
linewidth=0.8
)
plt.xlim(0, REC_INT * n)
plt.ylim(0.8, 1)
plt.xlabel('Step')
plt.ylabel('Performance')
plt.legend(('Accuracy',
#'Maximum Accuracy: {m[1]:.2%} at step {m[0]}'.format(m=acc_max),
'Recall',
#'Maximum Recall: {m[1]:.2%} at step {m[0]}'.format(m=rec_max),
'Precision',
#'Maximum Precision: {m[1]:.2%} at step {m[0]}'.format(m=pre_max),
'F-Score',
#'Maximum F-score: {m[1]:.2%} at step {m[0]}'.format(m=fsc_max)
))
plt.show()
if PDF:
fig_perf.savefig(SYS + '_nn_perf.pdf', bbox_inches='tight')
Prediction vs. actual failed components for a failure case
def plot_predict_test(case, w=0.3, threshold=0.5):
print('Initial Failures: {}'.format((np.nonzero(x_test[case])[0] + 1).tolist()))
fig_pred = plt.figure(figsize=(16, 5))
prd = plt.bar(np.arange(N_COMP) - w/2, sg_test[case], w)
act = plt.bar(np.arange(N_COMP) + w/2, y_test[case], w)
thr = plt.plot(np.arange(-1, N_COMP + 1), np.full(N_COMP + 2, threshold), ':k')
plt.xlabel('Components')
plt.ylabel('Failure Probability')
plt.xticks(np.arange(N_COMP), rotation=90)
plt.legend((prd[0], act[0], thr[0]), ('Predicted', 'Actual', 'Decision Threshold'))
plt.xlim(-1, N_COMP)
plt.show()
if PDF:
fig_pred.savefig(SYS + '_nn_' + str(case) + '_pred.pdf', bbox_inches='tight')
plot_predict_test(141, threshold=FAILURE_THRESHOLD)
Initial Failures: [1, 15, 16, 17, 84, 85, 95, 100]

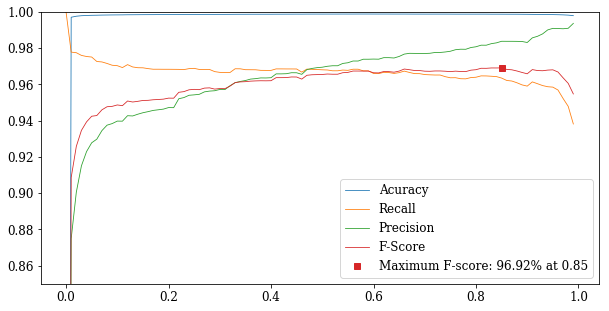
Find best decision threshold to maximize F-Score
def fscore_curve(start=0, stop=1, step=0.01):
p = []
threshold = np.arange(start, stop, step)
for t in threshold:
p.append(performance(y_valid, decision(sg_valid, t)))
acc = [x['accuracy'] for x in p]
rec = [x['recall'] for x in p]
pre = [x['precision'] for x in p]
fsc = [x['fscore'] for x in p]
fig_thr = plt.figure(figsize=(10, 5))
plt.plot(
threshold, acc, 'C0',
threshold, rec, 'C1',
threshold, pre, 'C2',
threshold, fsc, 'C3',
threshold[np.argmax(fsc)], np.amax(fsc), 'C3s',
linewidth=0.8)
plt.legend((
'Acuracy',
'Recall',
'Precision',
'F-Score',
'Maximum F-score: {:.2%} at {:.2f}'.format(np.amax(fsc), threshold[np.argmax(fsc)])))
plt.ylim(0.85, 1)
plt.show()
if PDF:
fig_thr.savefig('nn_threshold.pdf', bbox_inches='tight')
fscore_curve()